Hotline: 0974.626.115

Hỗ trợ tư vấn tuyển sinh

Trụ sở chính : 0964.626.115 - 0937.626.115

Số 81, ngõ 70, đường Phạm Thận Duật, phường Bích Đào, TP. Ninh Bình

Văn phòng tiếp nhận hồ sơ tại Tp HCM : 0983.995.116 - 0974.626.115

Số 168 bis Đường Phan Văn Trị, Phường 5, Quận Gò Vấp, Tp HCM

Văn phòng tiếp nhận hồ sơ tại Hà Nội : 0947.626.115 - 0937.626.115

Số 28, đường Vườn Cam, phường Phú Đô, quận Nam Từ Liêm, TP. Hà Nội T2-CN: 8h-18h

Hướng dẫn làm hồ sơ

Đăng ký tư vấn trực tuyến

Tin tức

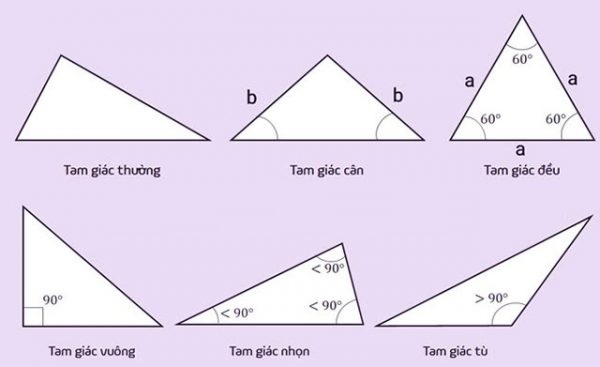
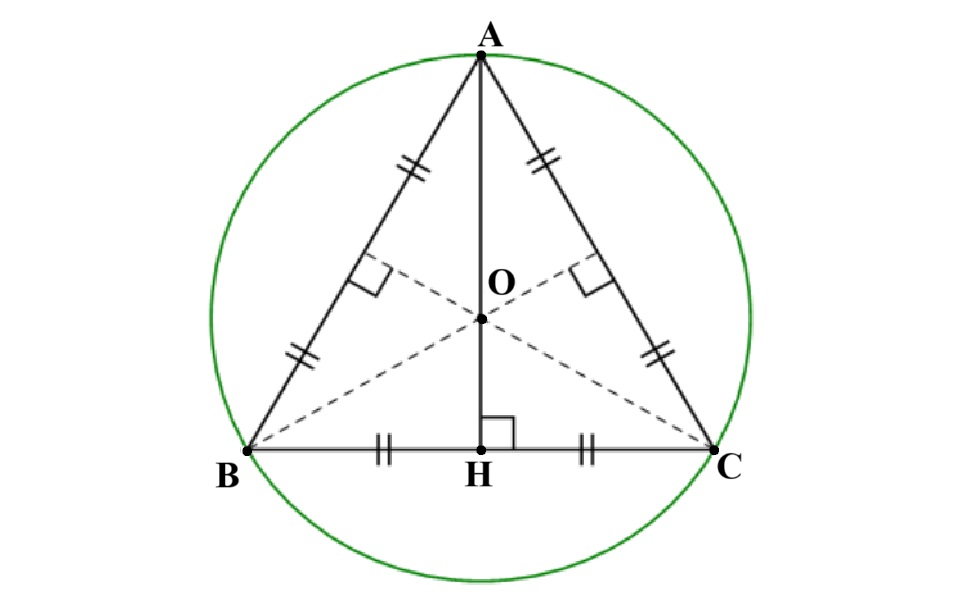
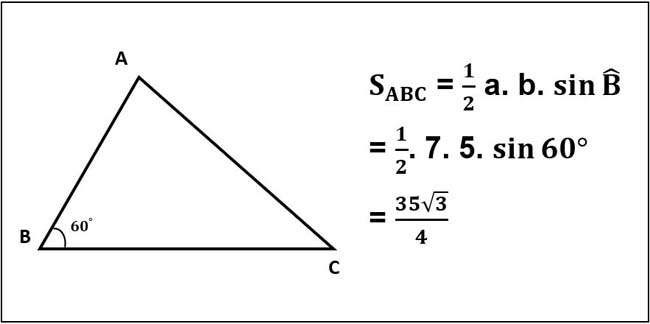
Công thức tính diện tích tam giác là gì? Có bao nhiêu cách tính?

Công thức tính diện tích tam giác là một khái niệm quen thuộc trong hình học. Việc tính toán diện tích tam giác có nhiều ứng dụng trong thực tế, từ việc tính toán diện tích đất đai đến các bài toán phức tạp hơn trong toán học.

[MỤC LỤC]

1. Hình tam giác là gì và phân loại
2. Các tính chất quan trọng của hình tam giác
3. Các công thức tính diện tích tam giác thường dùng
4. Các bài tập áp dụng công thức tính diện tích tam giác

Công thức tính diện tích tam giác

1. Hình tam giác là gì và phân loại

Hình tam giác là gì?

Hình tam giác là một hình phẳng được tạo bởi ba đoạn thẳng nối liền ba điểm không thẳng hàng. Ba điểm này gọi là các đỉnh của tam giác, và ba đoạn thẳng gọi là các cạnh của tam giác. Tam giác là hình đa giác đơn giản nhất và là một trong những hình học cơ bản.

Phân loại hình tam giác

Dựa vào độ dài các cạnh và số đo các góc, ta có thể phân loại tam giác thành các loại sau:
Tam giác thường:
Định nghĩa: Là tam giác có ba cạnh không bằng nhau và ba góc không bằng nhau.
Ví dụ: Hầu hết các tam giác chúng ta thường gặp đều là tam giác thường.
Tam giác cân:
Định nghĩa: Là tam giác có hai cạnh bằng nhau.
Tính chất: Hai góc ở đáy bằng nhau.
Ví dụ: Tam giác cân thường được sử dụng trong kiến trúc, xây dựng.
Tam giác đều:
Định nghĩa: Là tam giác có ba cạnh bằng nhau.
Tính chất: Ba góc bằng nhau, mỗi góc bằng 60 độ.
Ví dụ: Tam giác đều thường xuất hiện trong tự nhiên như các bông hoa, tinh thể.
Tam giác vuông:
Định nghĩa: Là tam giác có một góc vuông (90 độ).
Tính chất: Cạnh đối diện với góc vuông gọi là cạnh huyền, hai cạnh còn lại gọi là cạnh góc vuông.
Ví dụ: Tam giác vuông được ứng dụng rộng rãi trong toán học, vật lý và kỹ thuật.

Các loại tam giác

2. Các tính chất quan trọng của hình tam giác

Tổng ba góc trong một tam giác

Dù là tam giác nào: thường, cân, đều hay vuông, tổng ba góc trong của nó luôn bằng 180 độ.
Đây là tính chất cơ bản nhất và được áp dụng rộng rãi trong các bài toán hình học liên quan đến góc.

Bất đẳng thức tam giác

Một cạnh của tam giác luôn có độ dài nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài của hai cạnh đó.
Điều này đảm bảo rằng ba cạnh bất kỳ không thể tạo thành một tam giác nếu không thỏa mãn điều kiện trên.

Mối liên hệ giữa cạnh bất kỳ và góc đối diện

Góc lớn hơn trong tam giác sẽ đối diện với cạnh dài hơn. Ngược lại, cạnh dài hơn sẽ đối diện với góc lớn hơn.
Tính chất này giúp xác định mối quan hệ giữa các góc và các cạnh trong tam giác.

Đường trung trực của tam giác

Ba đường trung trực trong tam giác cắt nhau tại một điểm, điểm duy nhất đó được gọi là tâm đường tròn ngoại tiếp tam giác. Tâm này là điểm cách đều cả ba đỉnh của tam giác.

Đường cao

Ba đường cao trong tam giác cắt nhau tại một điểm, gọi là trực tâm.

Đường trung tuyến

Ba đường trung tuyến của tam giác cắt nhau tại 1 điểm duy nhất tại trọng tâm. Trọng tâm chia mỗi đường trung tuyến theo tỉ lệ 2:12:12:1, với phần dài hơn nằm về phía đỉnh.

Đường phân giác

Đường phân giác còn chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề.
Ba đường phân giác của tam giác gặp nhau tại tâm đường tròn nội tiếp tam giác – điểm cách đều các cạnh của tam giác.
Tham khảo: Bảng chữ cái Việt Nam

Tính chất nội tiếp của tam giác

3. Các công thức tính diện tích tam giác thường dùng

Công thức tính diện tích tam giác cơ bản

Nếu biết chiều cao h và độ dài cạnh đáy a, diện tích tam giác được tính bằng:
S = (a x h) / 2

Công thức sử dụng sin

Nếu tam giác có hai cạnh a và b cùng với góc C nằm giữa chúng:
S = (1/2)absinC = (1/2)bcsinA = (1/2)acsinB

Công thức sử dụng bán kính đường tròn ngoại tiếp

Khi bán kính R của đường tròn ngoại tiếp và độ dài ba cạnh a, b, c đã biết:
S = abc / 4R

Công thức Heron

Khi đã biết độ dài của cả ba cạnh a, b, c, có thể sử dụng công thức Heron, với p là nửa chu vi của tam giác:
S = √[p(p-a)(p-b)(p-c)]

Công thức sử dụng bán kính đường tròn nội tiếp

Nếu bán kính r của đường tròn nội tiếp và nửa chu vi p của tam giác đã xác định:
S = pr

Công thức sử dụng tọa độ

Nếu tọa độ của ba đỉnh tam giác là (x1,y1), (x2,y2), (x3,y3) ta có công thức:
S = (1/2)|x1(y2-y3) + x2(y3-y1) + x3(y1-y2)|

Công thức diện tích tam giác

4. Các bài tập áp dụng công thức tính diện tích tam giác

Bài tập 1: Áp dụng công thức cơ bản

Bài toán: Cho tam giác ABC có đáy BC = 8cm, chiều cao AH = 5cm. Tính diện tích tam giác ABC.
Giải:
Áp dụng công thức: S = (a x h) / 2
Thay số: S = (8 x 5) / 2 = 20 cm²

Bài tập 2: Áp dụng công thức sử dụng sin

Bài toán: Cho tam giác ABC có AB = 6cm, AC = 7cm và góc A = 60 độ. Tính diện tích tam giác ABC.
Giải:
Áp dụng công thức: S = (1/2)absinC
Thay số: S = (1/2) x 6 x 7 x sin60° ≈ 18.19 cm²

Bài tập 3: Áp dụng công thức Heron

Bài toán: Cho tam giác ABC có AB = 5cm, BC = 7cm, AC = 8cm. Tính diện tích tam giác ABC.
Giải:
Tính nửa chu vi: p = (5 + 7 + 8) / 2 = 10 cm
Áp dụng công thức Heron: S = √[10(10-5)(10-7)(10-8)] ≈ 17.32 cm²

Bài tập 4: Áp dụng công thức sử dụng tọa độ

Bài toán: Cho tam giác ABC có A(1, 2), B(3, 5), C(-2, 4). Tính diện tích tam giác ABC.
Giải:
Áp dụng công thức: S = (1/2)|x1(y2-y3) + x2(y3-y1) + x3(y1-y2)|
Thay số: S = (1/2)|1(5-4) + 3(4-2) + (-2)(2-5)| = 7.5 đơn vị diện tích

Bài tập 5: Áp dụng công thức liên quan đến đường tròn ngoại tiếp (Bài tập nâng cao)

Bài toán: Cho tam giác ABC nội tiếp đường tròn (O) có bán kính R = 5cm. Biết AB = 6cm, AC = 8cm. Tính diện tích tam giác ABC.
Giải:
Áp dụng công thức: S = abc / 4R
Tính BC (sử dụng định lý cos hoặc sin)
Thay số để tính diện tích

Bài tập 6: Áp dụng công thức liên quan đến đường tròn nội tiếp (Bài tập nâng cao)

Bài toán: Cho tam giác ABC có bán kính đường tròn nội tiếp r = 2cm, nửa chu vi p = 9cm. Tính diện tích tam giác ABC.
Giải:
Áp dụng công thức: S = pr
Thay số: S = 2 x 9 = 18 cm²
Trên đây là một số thông tin về công thức diện tích tam giác. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.

Tin tức liên quan

Bằng y sĩ đa khoa: Hành trang thiết thực trong ngành chăm sóc sức khỏe

Khám phá chương trình đào tạo bằng y sĩ đa khoa, điều kiện hành nghề, kỹ năng cần có và tiềm năng phát triển trong hệ thống y tế hiện đại – lựa chọn vững vàng cho người yêu thích ngành y.

Cao đẳng y học cổ truyền TP HCM: Hành trang cho tương lai nghề y

Bạn muốn học cao đẳng y học cổ truyền TP HCM? Khám phá môi trường đào tạo, cơ hội việc làm và lý do chọn Cao đẳng Y Dược Tôn Thất Tùng để theo đuổi ngành y truyền thống giữa lòng thành phố hiện đại.

Cao đẳng y học cổ truyền Hà Nội: Gìn giữ tinh hoa y học dân tộc

Khám phá chương trình đào tạo cao đẳng y học cổ truyền Hà Nội, cơ hội nghề nghiệp và lý do nên chọn học tại các trường uy tín để theo đuổi ngành y học cổ truyền.

Cao đẳng y học cổ truyền: Cơ hội nghề nghiệp bền vững trong y tế

Tìm hiểu chương trình đào tạo cao đẳng y học cổ truyền, cơ hội nghề nghiệp và lý do nên học tại Cao đẳng Y Dược Tôn Thất Tùng – trường uy tín đào tạo ngành Y tại Việt Nam.

Chứng chỉ hành nghề y sĩ răng hàm mặt: Điều kiện, thủ tục và pháp lý

Tìm hiểu đầy đủ về chứng chỉ hành nghề y sĩ răng hàm mặt: điều kiện cấp, quy trình đăng ký và vai trò pháp lý trong hoạt động chuyên môn nha khoa tại Việt Nam.

Các trường Cao đẳng Y sĩ đa khoa uy tín tại Hà Nội

Ngành Y sĩ đa khoa luôn là một trong những ngành học được nhiều bạn trẻ quan tâm và lựa chọn. Tại Hà Nội, có nhiều trường Cao đẳng Y sĩ đa khoa uy tín, cung cấp chương trình đào tạo chất lượng, đáp ứng nhu cầu nguồn nhân lực cho ngành y tế.

Lộ trình đào tạo y sĩ đa khoa hệ cao đẳng chi tiết

Ngành y sĩ đa khoa hệ cao đẳng đào tạo những cán bộ y tế có trình độ chuyên môn, kỹ năng thực hành tốt, có khả năng tham gia vào công tác khám chữa bệnh, chăm sóc sức khỏe ban đầu cho người dân.

Danh sách các trường trung cấp nghề điều dưỡng Hà Nội uy tín

Việc lựa chọn một trường trung cấp nghề điều dưỡng uy tín tại Hà Nội là bước đầu tiên quan trọng để bạn xây dựng sự nghiệp thành công trong lĩnh vực này. Dưới đây là danh sách các trường trung cấp nghề điều dưỡng Hà Nội uy tín, cùng với những thông tin chi tiết giúp bạn đưa ra quyết định sáng suốt.

Cơ hội việc làm với bằng y sĩ y học cổ truyền là gì?

Y sĩ y học cổ truyền là một ngành nghề đang ngày càng được quan tâm trong xã hội hiện đại, khi con người có xu hướng tìm kiếm những phương pháp chăm sóc sức khỏe tự nhiên và an toàn hơn. Với tấm bằng y sĩ y học cổ truyền, bạn sẽ có nhiều cơ hội việc làm hấp dẫn trong các lĩnh vực khác nhau.

Thông tin về chứng chỉ hành nghề y sĩ y học cổ truyền bạn nên biết

Chứng chỉ hành nghề y sĩ y học cổ truyền là văn bản pháp lý do cơ quan nhà nước có thẩm quyền cấp cho những người có đủ trình độ chuyên môn và đáp ứng các điều kiện hành nghề theo quy định của pháp luật. Sau đây sẽ cùng chúng tôi tìm hiểu về chứng chỉ này nhé!

Một số trường cao đẳng y dược cổ truyền uy tín

Ngành Y khoa luôn là một trong những ngành học được quan tâm hàng đầu tại Việt Nam. Bên cạnh các trường đại học danh tiếng, các trường cao đẳng y dược cổ truyền cũng đóng vai trò quan trọng trong việc đào tạo nguồn nhân lực y tế chất lượng cao.

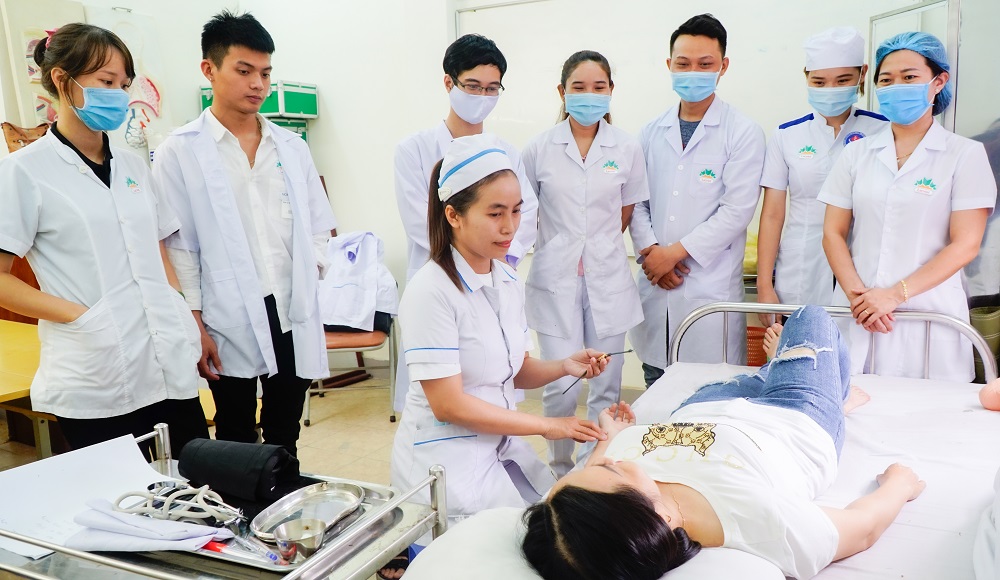
Bằng y sĩ đa khoa là gì? Thủ tục cấp bằng và cơ hội làm việc

Bằng Y sĩ đa khoa là văn bằng chứng nhận người sở hữu đã hoàn thành chương trình đào tạo chuyên ngành Y sĩ đa khoa. Văn bằng này chứng minh bạn đã được đào tạo chuyên sâu để có đủ năng lực chẩn đoán và điều trị bệnh, cũng như thực hiện các nhiệm vụ chăm sóc sức khỏe cơ bản cho cộng đồng.

Tin nổi bật